Instrumental Variables
Welcome
Introduction!
Welcome to our sixth tutorial for the Statistics II: Statistical Modeling & Causal Inference (with R) course.
During this week's lecture you reviewed what happens when experiments break due to non-compliance. You were also introduced to encouragement experimental setups, and their the observational analogue, instrumental variables. Finally, you learned how you can estimate local average treatment effects by breaking out the variation in D into two parts.
In this lab session we will:
- Review how to manually extract the LATE through the wald estimator
- Learn how to perform Two-stage Least Squares regression (2SLS) with
ivreg()from theAERpackage - Illustrate the mechanics of Two-stage Least Squares regression (2SLS) with
lm()
Packages
# These are the libraries we will use today. Make sure to install them in your console in case you have not done so previously.
library(tidyverse) # To load the collection of packages in the tidyverse
library(dplyr) # To wrangle our data (this package is also loaded by library(tidyverse))
library(readr) # To load the .csv data (this package is also loaded by library(tidyverse))
library(ggplot2) # To create plots (this package is also loaded by library(tidyverse))
library(tidyr) # To use pivot_wider() (this package is also loaded by library(tidyverse))
library(ggdag) # To dagify and plot our DAG objects in R
#library(summarytools) # for ctable()
library(broom) # To format regression output
library(janitor) # To examine our data with tabyl()
library(stargazer) # To format model output
library(knitr) # To create HTML tables with kable()
library(kableExtra) # To format the HTML tables
library(AER) # To run 2SLS with ivreg()Measuring the effect of mosquito net use on malaria infections
Imagine that the organization you work for is laying out a project to distribute mosquito nets to help combat malaria transmitions.
The funding agency requires a impact evaluation report from your organization. You are in charge of running the evaluation of this program.
You realize that there are potential unobserved counfounders that could bias the observed differences in malaria risk for mosquito net users and non-users. You also think about the ethical considerations of fully randomizing who receives the nets, so you remember your Statistics II lecture on IVs and set up an encouragement design.
Your benificiaries are scattered across ten villages. You decide to randomly select five villages to send SMS reminders every night encouraging them to use the mosquito nets. (This example is using simulated data)

Assumptions
To render credible results for the evaluation of this program, we need to fulfill a certain set of assumtions:
a) Relevance: Also known as non-zero average encouragement effect. Does our \(Z\) create variation in our \(D\)? In other words, is the mosquito net use different under the encouragement group? (Statistically testable)
b) Exogeneity/Ignorability of the instrument: Potential outcomes and treatments are independent of \(Z\). In this case given by out randomization of encouragement by villages.
c) Exclusion restriction: The instrument only affects the outcome via the treatment. In other words, there are no alternative paths through which our SMS can have an effect on malaria infections other that the use of the mosquito nets.
d) Monotonicity: No defiers. We assume that non-compliers fall in the camp of always- and never-takers. We would not expect subjects who when encouraged would not use the nets, but would use them if they did not recieve the SMS reminder.
Exploring our data
evaluation_df <- readr::read_csv("https://raw.githubusercontent.com/seramirezruiz/stats-ii-lab/master/Session%205/data/evaluation_data.csv") # loading simulated data frame of the interventionYou receive the results of your intervention from the M&E officers. There are 1000 inhabitants across the ten villages. This is what the data look like:
village_name: A character string with the name of the villagesms: A binary marker for the SMS encouragementnet_use: A binary marker for mosquito net usemalaria: A binary marker for malaria infection
Compliance types
You may remember, this table from the lecture:
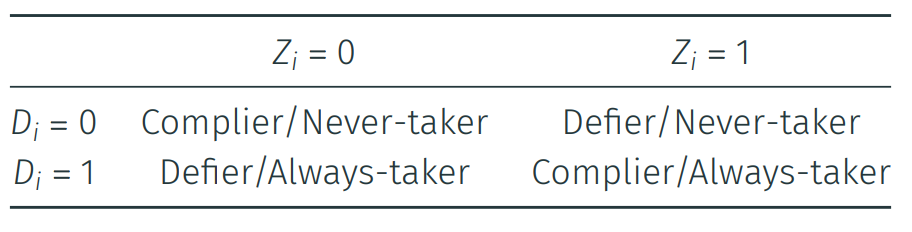
We can crosstabulate our data with janitor::tabyl() and the additional features of the janitor::adorn_* functions.
Why janitor::tabyl()? Because as prospective policy analysts we will do a lot of counting.
As the vignette of the package even puts it:
Analysts do a lot of counting. Indeed, it’s been said that 'data science is mostly counting things.' But the base R function for counting, table(), leaves much to be desired:
- It doesn’t accept data.frame inputs (and thus doesn’t play nicely with the %>% pipe)
- It doesn’t output data.frames
- Its results are hard to format. Compare the look and formatting choices of an R table to a Microsoft Excel PivotTable.
This is how it works. Say we are interested in exploring the number of persons in each of the observed strata, we would do:
evaluation_df %>% # your data frame
janitor::tabyl(net_use, sms) %>% # the two dimensions for the table (D, Z)
janitor::adorn_totals(c("row", "col")) %>% # add totals for rows and cols
knitr::kable() %>% # turn into a kable table for nice rendering in HTML
kableExtra::kable_styling() %>%
kableExtra::add_header_above(c("", "sms" = 2, "")) #add header for sms| net_use | 0 | 1 | Total |
|---|---|---|---|
| 0 | 335 | 110 | 445 |
| 1 | 165 | 390 | 555 |
| Total | 500 | 500 | 1000 |
If you want to learn more about the syntax of tabyl(), make sure to check the vignette
Exercise
- Where are our compliers and non-compliers?
- How many people were encouraged via SMS, but did not use the net?
- How many people were not encouraged via SMS, yet they utilized the net?
Average malaria infections across strata
We can utilize the tabyl() syntax and our knowledge from the grammar of graphics to table and visualize the distribution of malaria on each stratum:
Table: Count of malaria infections across strata (Y,Z)
evaluation_df %>% # your data frame
janitor::tabyl(malaria, sms) %>% # the two dimensions for the table (Y, Z)
janitor::adorn_totals(c("row", "col")) %>% # add totals for rows and cols
knitr::kable() %>% # turn into a kable table for nice rendering in HTML
kableExtra::kable_styling() %>%
kableExtra::add_header_above(c("", "sms" = 2, "")) #add header for sms
evaluation_df %>% # your data frame
janitor::tabyl(malaria, sms) %>% # the two dimensions for the table (Y, Z)
janitor::adorn_totals(c("row", "col")) %>% # add totals for rows and cols
knitr::kable() %>% # turn into a kable table for nice rendering in HTML
kableExtra::kable_styling() %>%
kableExtra::add_header_above(c("", "sms" = 2, "")) #add header for sms| malaria | 0 | 1 | Total |
|---|---|---|---|
| 0 | 248 | 410 | 658 |
| 1 | 252 | 90 | 342 |
| Total | 500 | 500 | 1000 |
Plot: Distribution of malaria infections across strata
ggplot(evaluation_df, aes(x = factor(sms),
y = factor(net_use),
color = factor(malaria))) +
geom_jitter() +
theme_minimal() +
scale_x_discrete(labels = c("SMS = 0", "SMS = 1")) +
scale_y_discrete(limits = c("1","0"), labels = c("NET = 1", "NET = 0")) +
scale_color_manual(values = c("#CDCDCD", "#CC0055"),
labels = c("Not infected", "Infected")) +
labs(x = "Encouragement",
y = "Treatment",
color = "") +
theme(legend.position = "bottom")
ggplot(evaluation_df, aes(x = factor(sms),
y = factor(net_use),
color = factor(malaria))) +
geom_jitter() +
theme_minimal() +
scale_x_discrete(labels = c("SMS = 0", "SMS = 1")) +
scale_y_discrete(limits = c("1","0"), labels = c("NET = 1", "NET = 0")) +
scale_color_manual(values = c("#CDCDCD", "#CC0055"),
labels = c("Not infected", "Infected")) +
labs(x = "Encouragement",
y = "Treatment",
color = "") +
theme(legend.position = "bottom")
Exercise
- What insights can we gather from the table and plot?
Exploring our set-up
Let's check whether SMS encouragement is a strong instrument
In other words, we are looking at the relevance assumption. Does our SMS encouragement create changes in our mosquito net use?
lm(net_use ~ sms, data = evaluation_df) %>%
stargazer::stargazer(type = "text")##
## ===============================================
## Dependent variable:
## ---------------------------
## net_use
## -----------------------------------------------
## sms 0.450***
## (0.028)
##
## Constant 0.330***
## (0.020)
##
## -----------------------------------------------
## Observations 1,000
## R2 0.205
## Adjusted R2 0.204
## Residual Std. Error 0.444 (df = 998)
## F Statistic 257.315*** (df = 1; 998)
## ===============================================
## Note: *p<0.1; **p<0.05; ***p<0.01Economists have established as a "rule-of-thumb" for the case of a single endogenous regressor to be considered a strong instrument should have a F-statistic 1 greater than 10. From this regression, we can see that SMS encouragement is a strong instrument.
Additionally, the substantive read in this case is that only 33% of those who did not receive the SMS utilized the mosquito nets, where as 78% of those who got the SMS encouragement did.
Let's gather a naïve estimate of mosquito net use and malaria infection.
Why do you think we call this a naïve estimate?
naive_model <- lm(malaria ~ net_use, data = evaluation_df)
stargazer::stargazer(naive_model, type = "text")##
## ===============================================
## Dependent variable:
## ---------------------------
## malaria
## -----------------------------------------------
## net_use -0.615***
## (0.023)
##
## Constant 0.683***
## (0.017)
##
## -----------------------------------------------
## Observations 1,000
## R2 0.415
## Adjusted R2 0.414
## Residual Std. Error 0.363 (df = 998)
## F Statistic 707.002*** (df = 1; 998)
## ===============================================
## Note: *p<0.1; **p<0.05; ***p<0.01Exercise
- What would our expectations be under the naïve model?
Let's gather our intent-to-treat effect (ITT)
This is the effect that our SMS encouragement had on malaria infections. \[ITT = E(Malaria_i|SMS=1) - E(Malaria_i|SMS=0)\]
itt_model <- lm(malaria ~ sms, data = evaluation_df)
stargazer::stargazer(itt_model, type = "text")##
## ===============================================
## Dependent variable:
## ---------------------------
## malaria
## -----------------------------------------------
## sms -0.324***
## (0.028)
##
## Constant 0.504***
## (0.020)
##
## -----------------------------------------------
## Observations 1,000
## R2 0.117
## Adjusted R2 0.116
## Residual Std. Error 0.446 (df = 998)
## F Statistic 131.753*** (df = 1; 998)
## ===============================================
## Note: *p<0.1; **p<0.05; ***p<0.01Exercise
- What does this tell us?
Let's gather out local average treatment effect (LATE)
We have several options for this:
- Wald Estimator We can calculate this by hand. Let's try that now using the values from the table we created earlier. We can also calculate the average malaria rates among those who did and did not receive an SMS (no SMS = 0.504, yes SMS = 0.18).
Table: Observations across strata (D,Z)
| net_use | 0 | 1 | Total |
|---|---|---|---|
| 0 | 335 | 110 | 445 |
| 1 | 165 | 390 | 555 |
| Total | 500 | 500 | 1000 |
Table: Count of malaria infections across strata (Y,Z)
| malaria | 0 | 1 | Total |
|---|---|---|---|
| 0 | 248 | 410 | 658 |
| 1 | 252 | 90 | 342 |
| Total | 500 | 500 | 1000 |
Local Average Treatment Effect (LATE) manually
\[LATE = \frac{cov(Y_i,Z_i)}{cov(D_i,Z_i)}\]
Let's take a look at our numerator \(cov(Y_i,Z_i)\), also \(ITT\)
\(E(Y|Z = 1) = \frac{90}{(410+90)} = 0.18\)
\(E(Y|Z = 0) = \frac{252}{(252+248)} = 0.504\)
Let's take a look at our denominator \(cov(D_i,Z_i)\)
\(E(D∣Z = 1) = \frac{390}{(390 + 110)} = 0.78\)
\(E(D∣Z = 0) = \frac{165}{(165 + 335)} = 0.33\)
We can calculate our LATE
\[LATE = \frac{(0.18 - 0.504)}{(0.78 - 0.33)} = -0.72\]
- Two-stage Least Squares (2SLS). We will learn how to do this with
ivreg(), which is part of theAERpackage. It fits instrumental-variable regression through two-stage least squares. The syntax is the following:
ivreg(outcome ~ treatment | instrument, data)In our case:
late_model <- AER::ivreg(malaria ~ net_use | sms, data = evaluation_df)
summary(late_model)##
## Call:
## AER::ivreg(formula = malaria ~ net_use | sms, data = evaluation_df)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.7416 -0.0216 -0.0216 0.2584 0.9784
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 0.74160 0.03089 24.00 <2e-16 ***
## net_use -0.72000 0.05159 -13.96 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.3671 on 998 degrees of freedom
## Multiple R-Squared: 0.4025, Adjusted R-squared: 0.4019
## Wald test: 194.8 on 1 and 998 DF, p-value: < 2.2e-16Exercise
- What is the substantive reading of these results?
- What would you tell the funding partner in your evaluation report?
Mechanics behind two-stage least squares (2SLS)
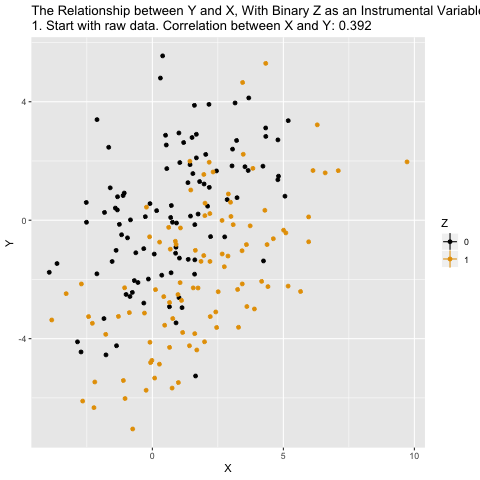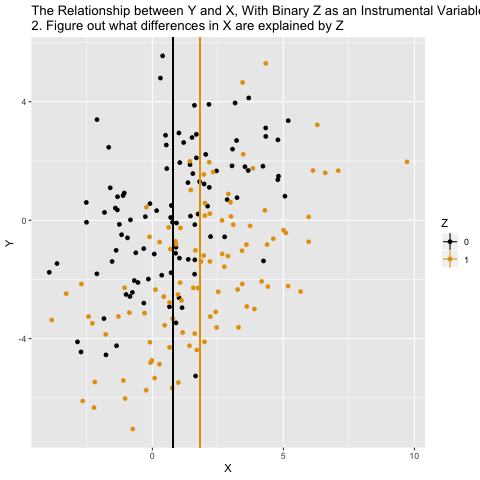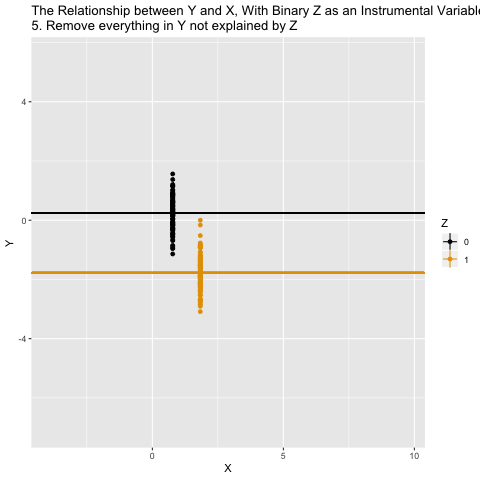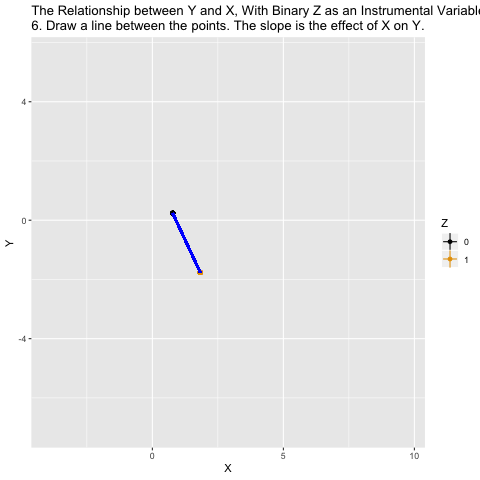
What ivreg() is doing in the background is the following:
net_use_hat <- lm(net_use ~ sms, evaluation_df)$fitted.values # get fitted values from first stage (the part of x that is exogenously driven by z)
summary(lm(evaluation_df$malaria ~ net_use_hat)) # run second stage with instrumented x (careful, the standard errors are wrong; better use ivreg() from AER instead)##
## Call:
## lm(formula = evaluation_df$malaria ~ net_use_hat)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.504 -0.180 -0.180 0.496 0.820
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 0.74160 0.03757 19.74 <2e-16 ***
## net_use_hat -0.72000 0.06273 -11.48 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.4463 on 998 degrees of freedom
## Multiple R-squared: 0.1166, Adjusted R-squared: 0.1157
## F-statistic: 131.8 on 1 and 998 DF, p-value: < 2.2e-16Thinking about the validity of instruments
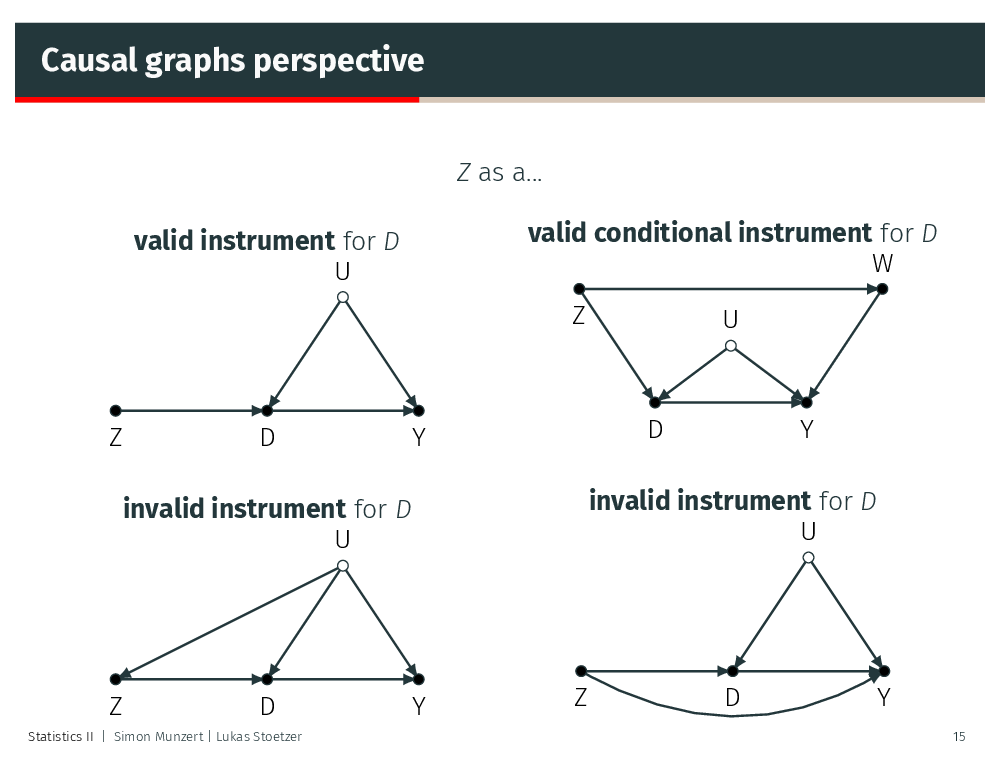
We can also adapt the ivreg() syntax to accomodate valid conditional instruments:
AER::ivreg(Y ~ D + W | Z + W, data = your_df)An F statistic is a value you get when you run an ANOVA test or a regression analysis to find out if the means between two populations are significantly different. It’s similar to a t-statistic from a t-test; A-T test will tell you if a single variable is statistically significant and an F test will tell you if a group of variables are jointly significant.↩